Quantum Computing

A qubit is either 0, 1, or somewhere in between.

Quantum Algorithms

Grover’s Algorithm

%%🖋 Edit in Excalidraw%%

Challenges

• Quantum states are very volatile
• Calls to $f$ have to be done in sequence, can’t be parallelised.

Application To Cryptography

%%🖋 Edit in Excalidraw%%

Shor’s Algorithm

%%🖋 Edit in Excalidraw%%

Applications to Cryptology

Can break Discrete Logarithm Problem, so it can also break Diffie-Hellman Key Exchange, ElGamal, etc.

Can also break integer factorisation, which means it breaks RSA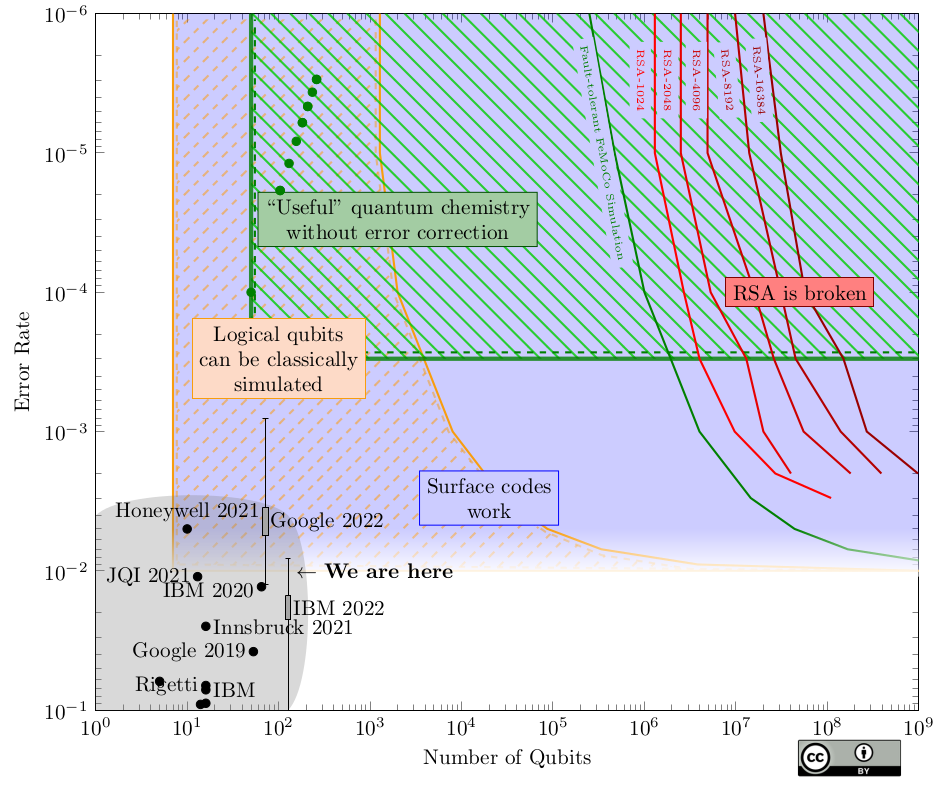

Impacts on TLS

• Block-ciphers (safe with scaled parameters)
• MACs (safe with scaled parameters)
• Hash-functions (safe with scaled parameters)
• Digital Signatures (broken, needs replacing)
• Group-based Key Exchange (broken, needs replacing urgently)

Replacing Key Exchange

We don’t know how to do NIKE - Non-interactive Key Exchange efficiently and post-quantum securely.

Instead, we are slowly moving towards KEM - Key Encapsulation Method, which we know how to do in more ways, including in ways that are quantum resistant.

Hard Problems we can use in PQ

• Error correcting codes
  • Short ciphertexts
  • Large public keys
• Cryptographic Lattices
  • fast
  • large-ish keys
• Isogenies
  • Very small keys
  • slow
• Hash based (signatures)
  • trusted security
  • very large and slow signatures
• Multivariate quadratic equations
  • Signatures only

Key Encapsulation

PQ algorithm is faster, but has much higher bandwidth consumption compared to ED25519

Signatures

Some have much larger key sizes, some have much larger signature sizes and higher signing time.